Our Products
Coordinate System Board Game
An engaging board game with a grid centered at (0,0), and -10 to +10 in X and Y directions. Players use two 20-face dice (white for Y, black for X) to determine coordinates. Students plot points and calculate the distance from the origin using the Pythagorean theorem, enhancing their understanding of coordinate systems and mapping.
Learn MoreTrig Ruler: Trigonometry in Motion

A unique ruler with Hypotenuse, Base, and Perpendicular scales, each 1 unit (100 smaller units) long. The Base and Perpendicular scales pivot on the Hypotenuse. A 0-360° circular disc is also attached. Students form a right-angle triangle by adjusting the Hypotenuse to an angle (0-90°). Cosine and Sine values are read directly from the Base and Perpendicular scales at their intersection.
Learn MoreThread Ruler & Multi-Function Drafting Instrument
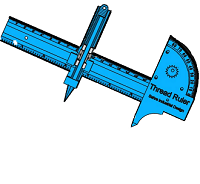
A single versatile instrument for drawing circles, ellipses, and parallel lines, doubling as a protractor, ruler, and drawing compass. It features a slide ruler holding a marking device and a stem with a thread. The thread attaches to the main ruler body for drawing ellipses. Usable on paper, drafting tables, chalkboards, and dry erase boards.
Learn MoreSky Tracker Planisphere: Global Star Locator
Our unique Planisphere combines a circular overlay star chart with a circular stereographic Earth map, connected at the center for free rotation. This allows users to view the night sky from any part of Earth by aligning the Right Ascension on the star chart with any Earth longitude on the stereographic map.
Learn MoreElliptical Bubble Leveler: Precision Angle
This innovative bubble leveler features a unique elliptical tube, unlike traditional designs. Its precisely curved tube ensures the bubble moves proportionally to the angle of inclination, directly indicating the exact angle on a clearly marked elliptical scale. This provides unparalleled accuracy and responsiveness for measuring angles on any surface.
Learn More3D-Compass: Pointing to Celestial Objects
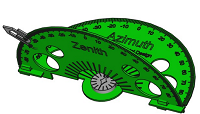
A tool to point to objects in a spherical coordinate system, like stars. Made of two semi-circle protractors (-90° to +90°), one for Declination/Zenith angle and the other for Right Ascension/Horizon, folded perpendicularly. The RA half has a magnetic compass, and the Dec half has a sliding arrow. Aligning the compass needle with RA and rotating horizontally places the Dec half in the star's plane; sliding the pointer to the star's declination then points to its direction.
Learn MoreCelestial Cup: Map of Stars on Your Desk
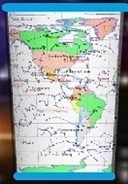
Map of the World printed on the inner glass and Constellation Map printed on the outer glass, together it's an interactive astronomical tool showing how the stars move when the world turns, bring the vastness of the cosmos right to your fingertips, a captivating way to understand celestial mechanics.
Learn More24-Hour Clock: World Map overlayed by Constellation Map

More than just a clock—it’s a dynamic, constant projection of your place in the universe.
Learn MoreConstellation Globe Planisphere
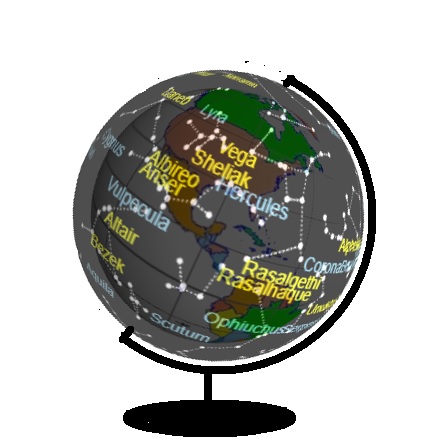
Visualize the entire celestial sphere surrounding the Earth in perfect 3D fidelity.
Learn MoreOur Mission
At Math & Astronomy Toolset, we're dedicated to transforming complex STEM concepts into engaging and accessible learning experiences. We believe that hands-on, intuitive tools are key to fostering deeper understanding and a lifelong passion for mathematics and science in high school students.
Our innovative products are designed to empower both teachers and students, providing practical ways to explore the wonders of coordinate systems, trigonometry, drafting, and celestial mechanics.