Unlock Your Creativity
Math & Astronomy Tools
Explore complex concepts with our innovative toolset. Our products, like the Planisphere and 3D Compass, provide a hands-on way to master math and astronomy.
View ProductsCAD & 3D Printing
Bring your ideas to life with our comprehensive training classes. Get hands-on experience with CAD software and 3D printers to learn the skills you need to create.
Explore ClassesWho We Are
We are dedicated to providing comprehensive educational tools and training that blend the fields of Math, Astronomy, and engineering design. Our mission is to empower students and enthusiasts to explore complex concepts in a tangible and creative way, using the power of Computer-Aided Design and 3D printing.
Coordinate System Board Game
A fun and interactive board game designed to make learning coordinate systems and spatial reasoning enjoyable. Students will navigate through a galaxy, plotting points and solving challenges to reach their destination.
Learn More
Trig Ruler
This innovative ruler is a visual and tactile tool for understanding trigonometry. It allows students to physically manipulate angles and measure the corresponding sine, cosine, and tangent values.
Learn More
Thread Ruler
A specialized ruler for engineers and designers. It accurately measures thread pitch and other complex dimensions, making it an essential tool for CAD and 3D printing projects.
Learn More
Elliptic Bubble Leveler
Not an ordinary Bubble Leveler, the bubble moves in an elliptic shape tube with indicies of degrees showing angle of inclination.
Learn More
3D Compass
This tactile 3D compass helps students understand and navigate three-dimensional space, a foundational concept for CAD and engineering.
Learn More
Celestial Cup Planisphere
Map of the World printed on the inner glass and Constellation Map printed on the outer glass, together it's an interactive astronomical tool showing how the stars move when the world turns,
Learn More
SkyTracker Planisphere
The SkyTracker is a classic educational tool for astronomy enthusiasts. It's a movable star chart that helps users identify visible constellations and stars at any given time and date.
Learn More Greenwich Mean Sidereal Time Interactive Planisphere24Hour Clock Planisphere
More than just a clock—it’s a dynamic, constant projection of your place in the universe.
Learn More Greenwich Mean Sidereal Time Interactive Planisphere
Constellation Globe Planisphere
Visualize the entire celestial sphere surrounding the Earth in perfect 3D fidelity.
Learn More Greenwich Mean Sidereal Time Interactive Planisphere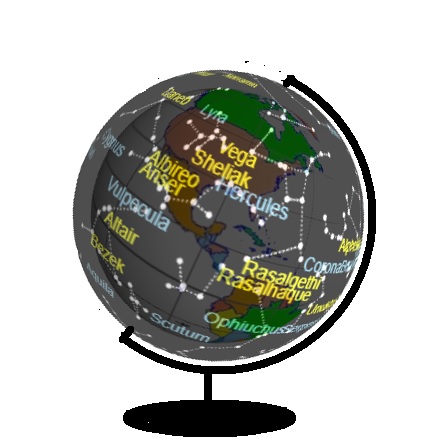
World Map Projections
A physical representation of various world map projections to demonstrate how a 3D globe is represented in 2D. This tool is essential for understanding cartography and the distortions inherent in different map types.
Learn More
Constellation Map Projections
Similar to the World Map Projections, this product visualizes how constellations and the night sky are mapped from a 3D sphere to a flat surface. It’s an advanced tool for aspiring astronomers and students of celestial navigation.
Learn More
Training Classes
Our comprehensive CAD and 3D printing courses are designed to unlock creativity and bring ideas to life. You'll gain hands-on experience with cutting-edge 3D printers and learn from expert instructors.
View CoursesCAD Foundations
Learn the core principles of Computer-Aided Design, from basic sketching and modeling to creating complex assemblies. Ideal for beginners.
- • Intro to CAD software
- • 2D sketching & constraints
- • 3D modeling techniques
Advanced 3D Printing
Go beyond the basics with our hands-on course that covers slicing, material science, printer calibration, and advanced techniques.
- • Slicing & print settings
- • Material properties & selection
- • Troubleshooting & maintenance
Get in Touch
Ready to learn more about our products or sign up for a class? Contact us today to start your creative journey.